참고: 이 포스팅에서는 상미분방정식만 다룬다.

미분방정식(differential equation, DE) 정의
> 하나 또는 둘 이상의 독립변수에 대해, 하나 또는 그 이상의 미지의 함수(또는 종속변수)의 도함수를 포함하는 방정식
배경지식1 미분식의 표기법
- 라이프니츠식 표기법:
독립변수와 종속변수가 명확한 장점이 있다.
- 프라임 표기법:
3계까지만 프라임으로 표현하고 4계부터는 위첨자 (4),(5)따위로 표현한다.
배경지식2 상미방의 미분형식 (differential form)
상미분방정식의 미분형식 (differential form)
상미분방정식의 미분형식 (differential form) [미분방정식의 표현1] y를 1계 상미방의 종속변수라고 가정한다면, 미분 dy는 dy=y'dx로 정의해야 함을 배웠다. 미분 dx로 양변을 나누거나 곱해서 어떤 미
splendidlolli.tistory.com
미분방정식의 분류
: 형태, 계수, 선형성으로 분류 가능하다. (type, order, linearity)
1. 형태에 의한 분류
형태에 따라 상미분방정식, 편미분방정식으로 분류가능하다.
이 포스팅에서는 상미분방정식만 다룰 것이다.
상미분방정식은 독립변수를 하나만 가지고, 편미분방정식은 독립변수를 두 개 이상 가진다.
상미분방정식 (ordinary DE)
하나의 독립변수에 대해 하나 또는 그 이상의 미지의 함수(또는 종속변수)의 상도함수만을 포함하는 방정식
상미분방정식의 예를 들어보자. (하나의 독립변수를 가진다)
......................................................

하나의 독립변수x | (종속변수 y)
........................................................

하나의 독립변수x | (종속변수 y)
........................................................

하나의 독립변수t | (종속변수 x,y)
.......................................................
2. 계수에 의한 분류
미분방정식의 계수: 방정식에서 가장 높은 도함수의 계수
1계, 2계, ..., n계 미분방정식
(참고: 1계 상미방은 종종 미분형식 M(x,y)dx+N(x,y)dy=0으로 쓰이기도 한다.)
3. 선형성에 의한 분류
ㅡ 함수 F가

에 대해 선형이면 n계 선형 상미분방정식이다.
ㅡ n계 상미분방정식

이

로 표현될 때, n계 선형 상미분방정식이라 부른다.
*가장 중요하고 특별한 경우는 1계선형, 2계선형이다.

선형 상미방의 특징
- 종속변수 y와 모든 도함수의 차수는 1이다. (각 항의 지수가 1이다.)
- y, y', y'', ..., y^(n)의 계수 a0, a1, ..., an은 기껏해야 독립변수 x에만 좌우된다.
선형 상미방의 예시를 들어보자.

비선형 상미방의 예시와 그 이유를 알아보자.
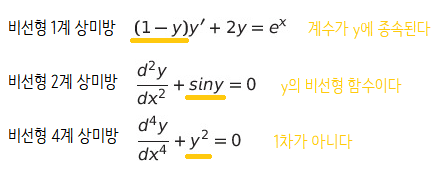
'수학 > 미분방정식' 카테고리의 다른 글
| 1계 변수분리형 미분방정식 | 특이해와 예제 하나 (0) | 2021.03.27 |
|---|---|
| 1계 변수분리형 미분방정식 | 일반해와 예제 하나 (0) | 2021.03.27 |
| 미분방정식 | 1계 초기값 문제 | 존재성과 유일성 (0) | 2021.03.18 |
| 미분방정식 | 초기값문제란? (0) | 2021.03.18 |
| 상미분방정식의 미분형식 (differential form) (0) | 2021.03.17 |
