로지스틱 회귀 모델을 이용해 A/B 클래스로 이진분류 하겠다고 하자.
로지스틱 회귀 모델이 다음과 같은 선형 방정식을 학습했다고 하자.
이 선형방정식이 어떻게 확률p와 연관되는지 알고싶다면 아래 이슈를 이해해야 한다!
▶ issue1) 이 선형방정식은 어떤 선형방정식을 학습한 것일까?
▶ issue2) z가 +면 양성클래스, -면 음성클래스로 분류한다.

개인적으로 왜 이 선형방정식이 확률 p와 연관이 되는지 바로 이해가 가지 않았다.
왜 이 z값을 logistic 함수에 대입하면 확률값으로 볼 수 있을까?
그래.. 그렇게 대입하면 0~1 확률로 말할 수 있는 값이 나오기는 하는데,
어떤 방식으로 z값이랑 확률p랑 의미있게 대응되는 것인지 느낌이 잘 안왔다. 무슨 관계길래..
간단히 정리해보았다.
# 사전 지식
[ 로지스틱 회귀를 이진분류 모델로 이용하는 원리 ]
내가 궁금한 샘플을 A/B 클래스로 분류하고자 할 때,
각 클래스일 확률을 계산해보고 가장 큰 확률인 클래스를 예측으로 내놓는다.
① 내가 넣은 샘플이 A클래스일 확률이 p라고 하자.
이 p를 구하는 것이 목적이다!
② 그런데 로지스틱 회귀모델이 학습한 것은 "선형방정식"이다.
선형방정식의 z값은 (-∞, ∞) 값을 가질 수 있다.
그러면 학습한 선형방정식을 사용해서 0~1 확률값을 도출해야 한다.
선형방정식 z를 logistic function에 대입하면 0~1범위로 보내버릴 수 있고, 그걸 확률값으로 사용한다.
# 왜 선형방정식을 logistic function에 대입하여 확률p를 얻는가?
확률에 관련된 정보 중, "오즈비"라는 것이 있다.
클래스 A로 분류하는 것을 "성공"이라고 두고, 그 성공확률은 p라고 하면, 다음이 오즈비다.

확률 p값은 [0, 1]범위고, 이에 따른 오즈비는 [0, ∞) 범위이다. (아래 그래프)

여기서 생각해볼 것은?
[0, 1] 범위인 p값과, (-∞, ∞) 범위의 어떤 값을 대응시킬 수 있어야 한다.
왜냐하면, 선형방정식의 z값이 (-∞, ∞)범위기 때문이다.
확률범위 [0, 1]과
선형방정식 z범위 (-∞, ∞)를 대응시킬 수 있다면
선형방정식을 통해 확률p를 알아낼 수 있지 않을까!
다음 단계로 고고
위 그래프에서 odds ratio의 범위가 0부터 ∞까지임을 확인했다.
odds ratio의 범위 [0, ∞)하면 생각나는 것은?
로그함수의 정의역이 생각난다! (0, ∞)
로그함수에다가 odds ratio를 합성시키자.
참고로 log(odds ratio)는 logit(p) 라고 표기함을 알아두자.
odds ratio 범위는 로그함수의 domain을 커버하므로,
확률값 p를 실수전체와 대응시킬 수 있겠다.
( p범위 ~ odds ratio범위 ~ log(odds ratio) = logit(p) = z )

엇 이 그래프를 회전해서 logit(p) = log(odds ratio)가 x축으로 가도록 바라보자.
와!! 그러면 domain은 실수전체고, range는 (0,1)이다.
어 여기서 domain인 z = log(odds ratio) 즉 logit(p) 함수가 '실수 전체' 범위라는 것에 주목하자.

'실수 전체 범위'인 logit(p) 에 따라서 p값이 대응되는 모습이 잘 보인다.
어 그런데!
실수 전체 범위인 선형방정식 z값도 실수 전체 범위에 대응된다.
그래서 다음과 같이 대응(~)시킬 수 있다.
(+ logit(p)와 선형방정식은 선형적으로 관련된다)
z = log(odds ratio) = logit(p) ~ 선형방정식
어!! 그러면!! 선형방정식을 통해 p를 구할 수 있겠다는 느낌이 온다.
# 선형방정식과 logit(p)가 대응(~)된다는 것은 알았다.
그런데 선형방정식이 어떻게 확률을 말해주지?
▶ 의문! 선형방정식은 데이터의 분포를 설명하는 식 아닌가?
logit(p)에 대응된다고 해서 확률p와 데이터분포가 무슨 상관인가?
▶ 이것을 확인하기 위해 Logistic Regression 모델이 학습하는 선형방정식을 직접 시각화해보았다.
특성 두가지를 통해 A클래스(0)인지 B클래스(1)인지 분류하는 로지스틱 회귀모형이 학습한 선형방정식이다.
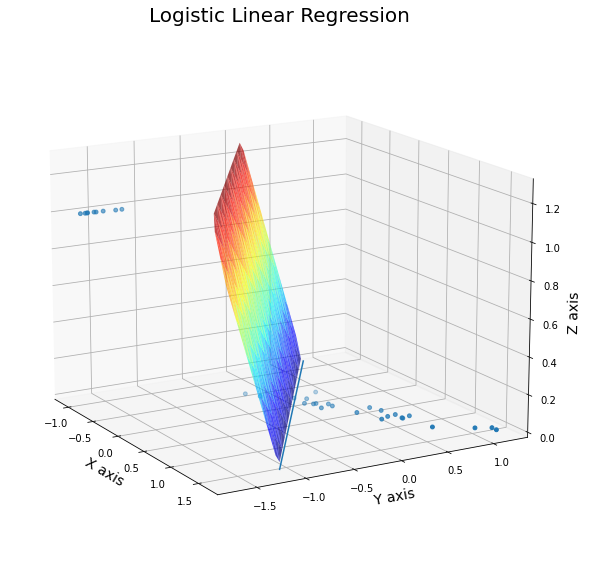
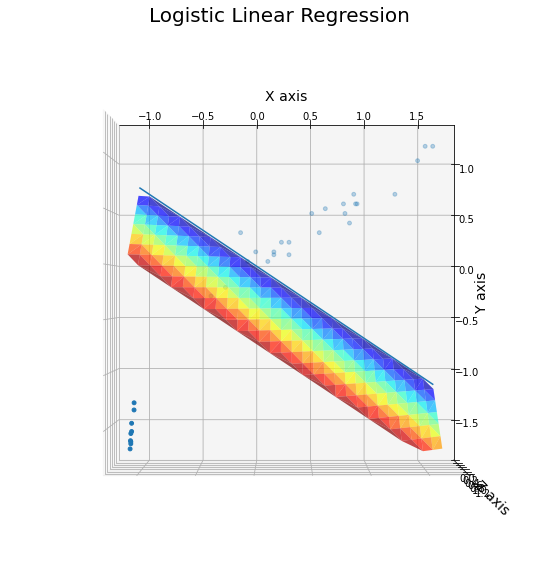
아..! 선형방정식을 이렇게 학습했구나!!
와 이렇게 보니까 직관적으로 이해가 간다. 다음을 이해해보자.
① 평면으로부터 수직거리가 먼 데이터일수록 A클래스(혹은B클래스)인 경향이 세다.
② 시각화 그림에서 평면(선형방정식) z는 (-∞, ∞)에서 값을 가지는 선형방정식으로서 logit(p)와 대응된다.
③ 하지만 선형방정식 자체로는 확률을 나타낼 수 없다. 그러나 logit(p)와 대응시켜서 logit(p)를 정의역으로 하고 확률p를 치역으로 하는 함수를 생각하면, 선형방정식으로 확률을 설명할 수 있다.
④ 로지스틱 회귀분석의 이진분류모델은 양성클래스에 대한 z값을 사용한다. 회귀방정식에 샘플을 넣어 양수가 나오면 양성클래스이다. 여기서 양수값이 크면 양성클래스일 확률(경향)이 높다는 것을 이해하자.
⑤ 선형방정식을 logit(p)에 대응시키고 다시 생각해보자. z값이 클수록 확률이 1에 수렴한다!

[ 이제 이해가 가는 것 ]
- 선형방정식이 왜 확률과 관련이 있는지 알았다.
- z값이 양수면, (logit(p)그래프에 의해) 확률p가 0.5 이상이므로 양성클래스라고 분류한다.
- 같은 맥락으로 z값이 음수면 음성클래스라고 분류한다.
여기까지 느꼈다면 거의 다했다.
수식으로 슉 알아보자.
왜 logisitic 함수에 선형방정식 z값을 대입하면 바로 확률p가 나오는지를 확인하자 ↓
먼저 큼직큼직하게 확인!
이렇게 회색박스끼리 서로서로 찾아갈 수 있는 느낌을 갖자.
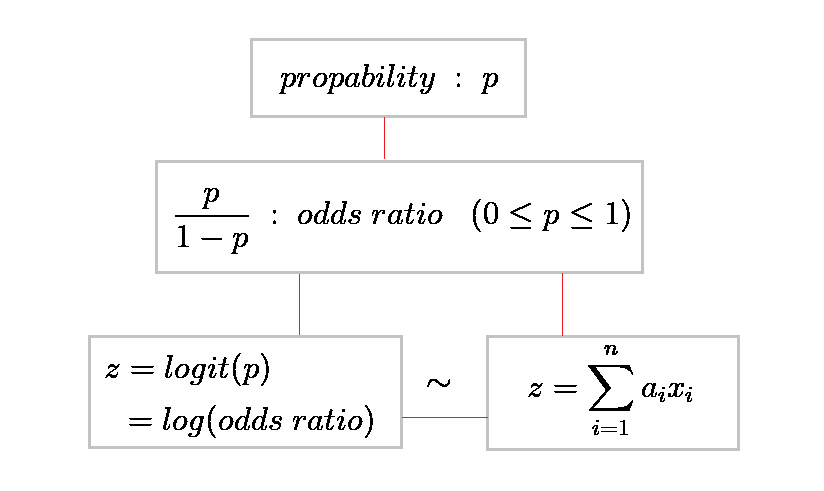
그럼 로지스틱 회귀모델이 학습한 "선형방정식"에서 어떻게 "확률p"를 도출할까?
아래 과정만 이해하면 끝이다!
아하 결국 "선형방정식이랑 logit(p)랑 대응된다"는 것만 이해하면,
선형방정식으로 확률 p를 도출하는 과정이 이해가 간다.
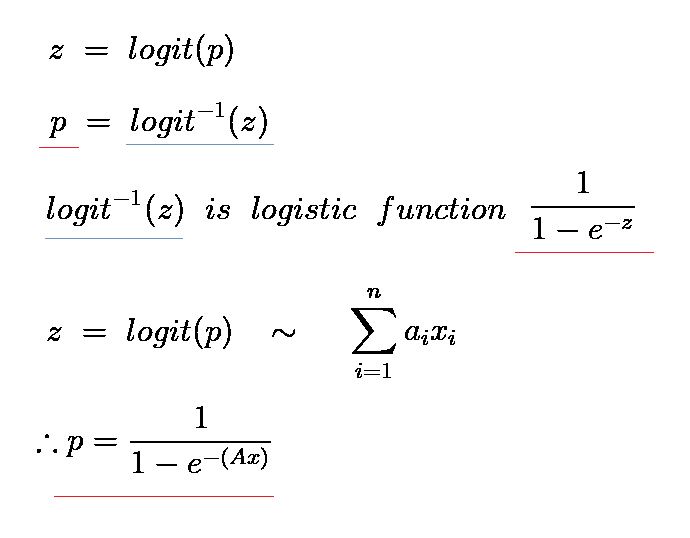
아하.. A클래스인지 판별하는 선형방정식에 test샘플을 넣고 z값을 얻으면,
그 z값이 위와 같은 과정으로 변환되어서 A클래스일 확률을 말해주는 거구나.
logit(p)의 역함수가 logistic function이구나.
여기서 한가지 더!
로지스틱 회귀모델에서 z값을 얻을 때 decision_function()이라는 메서드를 사용했다.
왜 z값을 얻는 메서드 이름이 decision function일까?
아래 그래프를 보면, z값에 따라 p의 범위가 나뉜다.
if z = 0, p = 0.5
if z > 0, p > 0.5 => y_hat = 1
if z < 0, p < 0.5 => y_hat = 0

z를 구하는 메서드가 decision_function() 이라는 이름인 이유도 여기에 있다.
z가 바로 분류모형의 판별함수(decision function) 역할을 하는 것이다.
+
+
로지스틱 회귀모델로 이진분류를 할 때에는 logistic function (sigmoid)를 사용했다.
A클래스에 대한 선형방정식 z값을 확률로 변환하여, A가 맞다 아니다로 분류하는 모델!
▶ 그러나 다중분류시에는 softmax function을 사용한다.
각 클래스에 대한 선형방정식 z에 대하여 exp(z)를 계산하고,
각 e_i를 e_sum으로 나눈 값을 확률값으로 취한다.
▶ 그럼 이번에는
"왜 exp(x)에 선형방정식 z를 대입하여 확률로 이용할 수 있는가?" 이게 궁금포인트네
간단히 상상해보고 끝내자.
exp는 실수전체 domain에서 (0, ∞)의 range를 갖는다.
아 그러면 선형방정식 z를 domain에 대응시킬 수 있고, 이를 (0, ∞)로 보내버릴 수 있다.
그러면 각 클래스의 선형방정식 z에 대하여 exp(z)를 계산하고
모든 클래스에 대한 비중을 따져보면 (즉 exp(z)/e_sum)
모든 클래스 확률 합이 1이도록 각 클래스 확률을 만들어낼 수 있겠구나!
이렇게 포스팅을 마친다.
🔑를 얻었다!! >ㅅ<
혹시 애매모호하거나 잘못된 내용 있으면 꼭! 알려주세요!
처음으로 공부한 내용이라 비약이 있을 수도 있겠습니다.
감사합니다
'데이터분석과 머신러닝' 카테고리의 다른 글
| 머신러닝 | 확률적 경사 하강법 (0) | 2022.01.30 |
|---|---|
| 혼공단 7기 3주차 미션인증 (0) | 2022.01.30 |
| 머신러닝 | 로지스틱 회귀모델 | 이진/다중분류 (0) | 2022.01.27 |
| 머신러닝 | 선형회귀모델 규제 - 과대적합 피하기 | 릿지/라쏘 회귀 (0) | 2022.01.24 |
| 머신러닝 | 특성 수를 늘려 과소적합 피하기 - 다중회귀와 특성 공학 (2) | 2022.01.23 |