한빛미디어 도서 <혼자 공부하는 머신러닝+딥러닝>의 전개를 따른 내용이다.
이번에 다룰 내용은 "다중 회귀와 특성공학"이다.
[ 요약 먼저 하자면 ]
다중회귀는 특성수가 많은 선형회귀이고,
특성공학은 기존의 특성을 활용해 새로운 특성을 만들어내는 작업이다.
특성 수를 늘리면 모델이 복잡해져 과소적합을 피할 수 있다.

챕터 3, 회귀 알고리즘과 모델 규제
| 다중 회귀, 특성 공학, 과소적합 피하기
* 지도 학습 알고리즘의 한 종류인 회귀 알고리즘 배우기
* 다양한 선형 회귀 알고리즘의 장단점 이해하기
선형회귀를 배우면서,
지금까지는 단 하나의 특성 length만 가지고 weight를 예측했다.
그렇지만 선형회귀는 특성이 많을수록 선형회귀능력이 강해진다!
이번에는 height와 width도 추가적으로 고려해 weight를 예측해보려고 한다!
# 다중회귀 <- 오늘의 핵심 키워드!
: 여러 개의 특성을 사용한 선형 회귀
공간적으로 떠올려보면 더 느낌이 잘 오고 재미있다.
◆ 특성 하나만을 학습하면 직선을 학습한다. y = ax + b
◆ 특성 두개를 학습하면 평면을 학습한다. z = ay + bx + c
◆ ... (4차원부터는 상상 불가이므로 생략)
특성이 늘어날수록 차원이 늘어나는 것이다. 다중회귀모델이 점차 복잡해져간다.
잠깐! 다중회귀모델이 복잡해지면 train set에 특정해서 세밀한 학습을 하게 된다. 그래서 train set에 대해서는 아주 높은 score()값을 얻을 수 있다. 그러나 test set의 score()는 아주 낮을 수 있다. 당연하다. 모델이 아주 복잡해지면 train set에 과대적합되기 때문이다.
.
.
# 특성 공학
기존의 특성을 사용해서 새로운 특성을 뽑아내는 작업을 말한다.
예를들면 기존의 특성1이 가로고 특성2가 세로면,
가로 x 세로 = 면적
면적이라는 특성3이 도출된다.
ㄴ 우리는 이 특성공학이라는 개념도 실습에 녹여 볼 것이다.
ㄴ 특성이 많을 수록 모델의 score는 어떻게 되는지 확인할 것이다.
# 데이터 준비하기
① 데이터를 불러오쟈
- 인터넷에서 csv파일을 내려받자. 판다스의 도움을 받아 읽을 수 있다.
이번에 input data에서 특이한 점은 "특성이 여러개"라는 것이다.
( 이전에는 특성이 length 하나뿐이었다. )

② train/test set으로 나눠놓쟈
train_test_split(perch_full, perch_weight, random_state = 42)
예측변수(입력변수)는 위에서 만들어둔 perch_full 데이터를 사용할 것이고,
반응변수(타겟변수)는 이전과 동일하게 perch_weight 데이터를 사용할 것이다.
perch_full 데이터는 농어의 여러 특성을 가진 input data다. (length, height, width)

잠깐! 이게 data준비 끝이 아니다.
우리는 지금 다중회귀를 공부하고 있기 때문에 "많은 특성"을 고려해야 한다.
물론 지금 perch_full 이라는 넘파이배열은 [length, height, width] 라는 세가지의 특성을 가지고 있지만,
우리는 기존 특성을 활용해 새로운 특성을 만들어 사용할 것이다. (위에서 언급한 특성공학)
특성이 많아지면 어떤 현상이 나타나는지 이어서 학습해보자.
# 특성이 많아진다면 무슨일이?
새롭게 특성을 만들어낼수록 차원이 높아지는데, 이는 모델을 복잡하게 만든다.
그런데 수많은 train set의 특성들로 모델을 학습시키면 과대적합될 수 있다!
그럼 어디 한번..
여러 개의 특성을 사용해서 선형회귀모델을 훈련시켜보자.
잠깐!!
특성을 많이 만들기 위해서 "변환기" 클래스를 사용한다.
사이킷런의 변환기 클래스 중에서 PolynomialFeatures를 이용할 것이다.
관련 설명은 접은글!!

원래 기존에 2와 3이라는 특성이 있었는데,
변환기 클래스 PolynomialFeatures를 거치면서
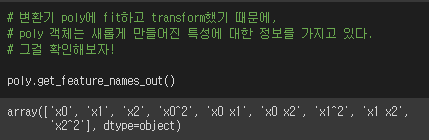
특성을 제곱하거나 특성끼리 곱해서 새로운 특성을 만들어냄을 볼 수 있다.
새로운 특성 1, 2, 3, 4, 6, 9 를 만들어냈다.
특성을 만드는 방식을 좀 더 이해가 쉽도록 설명해보겠다.
기존 특성을 ②, ③이라고 하자.
그럼 '특성 공학'은 다음과 같은 식으로 설명 가능하다.
new특성 = □②^2 + □② + □③^2 + □③ + ㅁ②③ + □1
기존 특성 ②, ③을 활용해서 new특성을 만들어내는 모습! 와우~ ^-^*
위 선형방정식을 잘 보면, 절편이 □*1이다. 선형방정식에서는 언제나 □라는 절편이 존재할텐데 (0이더라도), 이 □라는 수를 □*1로 바라보면!! 1이라는 특성과 곱해지는 계수가 □인 것을 확인 가능!
아아~~ 그러면 특성에 1은 항상 포함시킬 수 있겠다.
그런데 1이라는 특성은 오직 절편을 위한 특성이므로, 제거해도 상관없다.
왜냐하면 사이킷런 선형 모델이 알아서 절편을 계산하기 때문이다. (모델 파라미터 개념을 떠올려라!)
include_bias=False 속성을 넣으면 된다.
(사실 1이 있더라도 선형모델이 알아서 거른다)

# 특성이 많아지면 어떻게 되는지 확인하자
기존의 input 데이터에 있는 특성은 length, height, width다.
이 기존 특성들을 통해 새로운 특성들을 만들어보자.
새로운 특성을 추가한 배열은 train/test_poly에 할당했다.
열의 크기가 3개였는데 9개로 늘었다.

그럼 이제 특성을 9개로 늘린 train_poly 데이터로 LinearRegression 모델을 학습시켜보자.
[ 결과 ]
◆ train set의 score가 높게 나왔다.
- length 특성 하나만 이용했을 때는 R^2가 약 0.97이었다.
- 하지만 9개의 특성을 이용하면 R^2가 약 0.99다.
즉, 특성이 많으면 선형회귀의 능력을 높일 수 있다.
◆ train set score > test set score 이다.
- length 특성 하나만 보았을 때 살짝 과소적합 문제가 나타났는데,
- 특성 수를 늘려서 모델을 복잡하게 만들었더니 과소적합 문제를 피했다.

.
.
참고) 특성수를 훨씬 많이 늘리면?
- 충분히 예상할 수 있다. 당연히 train score는 엄청 높게 나올 것이다.
- 다만 과대적합되어서 test score는 극히 낮게 나올 것이다.
이번 글에서는 과소적합을 피하는 방법으로 '특성 수 늘리기'를 새로 배웠다
다음 글에서는 과대적합을 피하는 방법을 공부해보자 >ㅅ<.......
글이 너무 길어질 것 같아서 분리한다..
# 이번 내용 정리
- 다중 회귀 : 여러개의 특성을 이용한 선형회귀
- 특성 공학 : 기존 특성을 활용해 새로운 특성을 만들어내는 방법
- 과소적합을 피하려면 모델을 복잡하게 해야 한다.
- 특성수를 늘리면 모델이 복잡해진다.
이전 글:
머신러닝 | 선형 회귀 알고리즘 (k-최근접이웃 알고리즘과 비교)
다음 글:
'데이터분석과 머신러닝' 카테고리의 다른 글
| 머신러닝 | 로지스틱 회귀모델 | 이진/다중분류 (0) | 2022.01.27 |
|---|---|
| 머신러닝 | 선형회귀모델 규제 - 과대적합 피하기 | 릿지/라쏘 회귀 (0) | 2022.01.24 |
| 혼공단 7기 2주차 미션인증 (0) | 2022.01.23 |
| 머신러닝 | 선형 회귀 알고리즘 (k-최근접이웃 알고리즘과 비교) (0) | 2022.01.22 |
| 머신러닝 | 회귀 모델 (+ knr) | 과소적합, 과대적합 (0) | 2022.01.21 |