
챕터 4, 다양한 분류 알고리즘
* 로지스틱 회귀, 확률적 경사 하강법과 같은 분류 알고리즘 배우기
* 이진 분류와 다중 분류의 차이를 이해하고 클래스별 확률을 예측하기
로지스틱 회귀!
드디어 로지스틱 회귀를 공부할 차례다 ~.~
[ 학습한 내용 요약 ]
- 어떤 클래스인지 분류해주는 모델을 공부했다
- k-최근접이웃 분류 모델은 확률산출에 한계가 있다
- 로지스틱 회귀모델을 분류모델로 사용 가능하다
- 이진분류 - sigmoid(logistic)
- 다중분류 - softmax
# k-최근접이웃 분류모델의 한계
k-최근접이웃 분류 모델은 확률 산출에 한계가 있다.
ex) 이웃개수 5개로 설정했다면 산출가능 확률은 0, 20, 40, 60, 80, 100 뿐이다.
딱 봐도 확률이 한정적이다.
참고) 실습에 사용한 데이터
① 데이터 부르기 / 데이터 확인하기
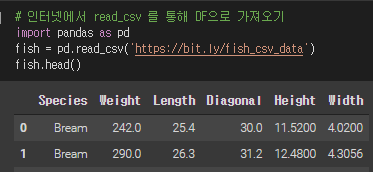
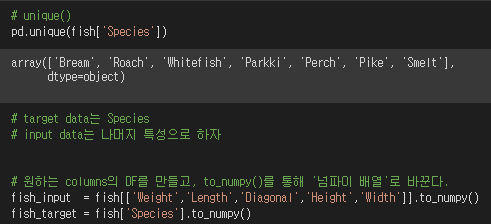
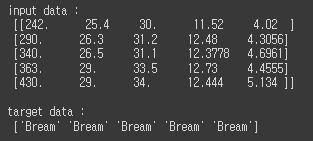
② train/test set

여기서 문든 든 생각.
train/test set을 나눠버리기 전에 scale을 맞추면 더 간단하고 편하지 않나?
=> 땡!!
train input으로 StandardScaler 객체를 fit해야 하므로.. 먼저 쪼개는 것이 맞다.
"먼저 train/test 쪼개야지" train_input으로 fit할 수 있다는 점만 기억하면 잊을 일 없겠다.

▶ 실습내용:
k-최근접이웃 모델로 예측해보고자 한다.
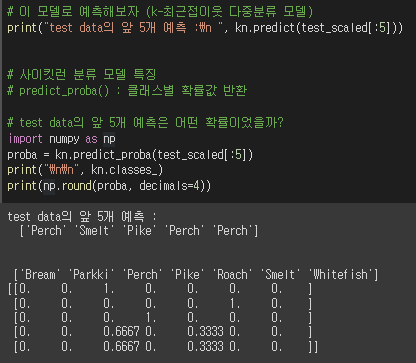
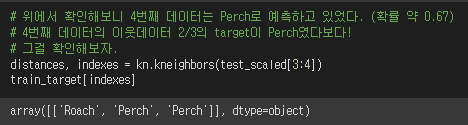
이처럼 Perch가 4번째데이터의 최근접이웃 3개중 2개의 target이었기 때문에,
2/3의 확률로 4번째 데이터의 target을 Perch라고 예측했던 것이다.
▶ 실습요약:
사이킷런 모델의 predict_proba()로 target 예측 확률을 확인해볼 수 있었다.
4번째 test 데이터의 이웃데이터 3개중에 2개가 Perch였기 때문에 가장 확률이 높았다.
그래서 target을 Perch라고 예측했다.
[ 확률 산출의 한계점 ]
◆ k-최근접이웃 분류모델은 오로지 '최근접이웃'만 이용하여 확률을 산출한다.
◆ 그래서 가능한 확률은 최근접이웃 개수에 따라서 한정된다.
# 로지스틱 회귀
로지스틱 회귀는 회귀문제, 분류문제 모두 가능하다.
그럼 확률에 한계가 있는 최근접이웃 모델은 버리고, 로지스틱 회귀모델로 분류해보도록 하자.
>> 로지스틱 회귀 알고리즘은 선형 방정식을 학습한다.
z = a(특성1) + b(특성2) + c(특성3) + d(특성4) + e(특성5) + f
>> 이 선형 방정식으로 어떻게 분류할 수 있을까?
① 특성데이터와 계수 a, b, c, d, e, f에 의해서 z값은 어떤 값이 된다.
② 그 z 값으로 '확률'을 보여줄 수 있다면 분류모델로서 사용 가능하다.
③ 확률은 [0, 1] 구간의 값이다.
④ z를 [0, 1] 구간 값으로 변환시키기 위해 sigmoid function을 사용한다.
⑤ sigmoid function 값 기준에 따라 클래스를 분류한다.
자세한 내용은 여기 : 로지스틱 회귀 | 선형방정식이 확률p가 되는 과정은?
.
.
시그모이드 함수 (로지스틱 함수)

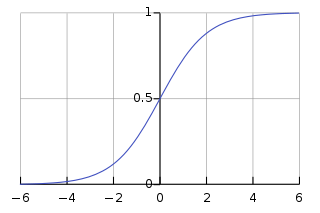
실습 : sigmoid 함수 직접 그려보기
.
.
아직까지 아리까리한 부분:
그럼 z값이 sigmoid에 합성되어 어떤 확률값을 내놓으면,
그 값으로 어떤클래스인지는 어떻게 안다는 말이지!??!
로지스틱 회귀로 분류 작업을 직접 해보며 알아보자.
먼저, 간단한 이진분류를 해보고
그 다음 다중분류를 해보자.
# 이진분류 - LogisticRegression
도미랑 빙어만 가지고 이진분류 실습 진행!
이진분류의 경우 음성클래스와 양성클래스로만 분류하면 된다.
※ 클래스명의 알파벳순으로 음성 / 양성이다.
Bream : 음성클래스
Smelt : 양성클래스
▶ 어떤 클래스로 예측할까?
회귀모델 lr을 이용해 predict해본 결과를 볼 수 있고,
predict_proba() 메서드로 확률값을 직접 확인할 수 있다.
음성클래스(Bream)으로 예측한 확률값,
양성클래스(Smelt)으로 예측할 확률값을 각각 확인가능하다.

▶ 확률값은 어떻게 산출될까?
회귀모델의 선형방정식 계수값과 상수항, 그리고 z값을 확인가능하다.
그리고 그 z값을 sigmoid와 합성한 결과 phi 는 확률값이다.
◆ 0 <= phi <= 0.5 : 음성클래스로 분류
◆ 0.5 < phi <= 1 : 양성클래스로 분류

▶ 책의 설명 : decision_function() 메서드는 양성 클래스에 대한 z값을 계산한다고 되어있다.
▶ 유추해보기 : z값을 sigmoid에 합성한 결과는 양성클래스에 대한 확률이다.
그러면 predict_proba()가 리턴하는 음성/양성 클래스에 대한 확률값은 이렇게 계산되리라 유추한다.
- 양성클래스에 대한 확률 = expit(z값)
- 음성클래스에 대한 확률 = 1 - expit(z값)
어 근데 이 z값은 우리가 초반에 z = ax1 + bx2 + c 에서 봤던 그 선형방정식 z값을 의미하는 것이긴 한데,
그 z = ax1 + bx2 + c의 z값을 어떤 원리로 확률로 사용하는가 고민해보았는데 뭔가 상상이 잘 안되더라..
다시말해서 특정 클래스의 분포를 말하는 선형방정식에 어떤 샘플 특성을 대입한 z값이 왜 확률인지 도저히 이해가 안되었다. 그래서 공부를 좀 열심히 해봤다.... ↓
이진분류는 양성/음성 클래스 두개뿐이라 뭔가 z값에 대한 분류가 간단해 보인다.
그냥 sigmoid에 z값을 합성해서 0.5를 기준으로 양성/음성 클래스로 분류한다.
그런데 다중분류는 도대체 분류기준이 어떻게 되는 거지?
상상이 잘 안 된다!
# 다중분류 - LogisticRegression
▶ LogisticRegression의 파라미터
LogisticRegression(C, max_iter)
매개변수에 대한 설명:
▷ max_iter
로지스틱 회귀도 라쏘모델(지난번에 배운 선형회귀 규제모델)처럼 반복적인 알고리즘이므로, 충분한 반복 횟수를 주어야 한다.
▷ C (규제 조절을 위한 매개변수)
LogisticRegression은 L2 규제를 사용한다.
L2 규제: 계수의 제곱을 규제
직전에 배운 릿지의 규제방법 또한 L2규제다.
릿지 규제 조절을 위해 alpha 하이퍼 파라미터를 이용했었다.
→ alpha가 클수록 규제가 크다
LogisticRegression에서는 규제 조절을 위해 C라는 하이퍼 파라미터를 이용한다.
→ C가 작을수록 규제가 크다 (기본값 1)
책 설명에 L2규제가 계수의 제곱을 규제한다는 말이 있었다.
그래서 L2 규제를 파보다가,,, 얘기가 길어졌다.
▶ 추가학습 : [ 규제, L2 Regularization]
① 규제에 대한 공통적인 사항
좋은 회귀 모델 : 다항 회귀의 Degree 이슈를 잘 해결하는 모델
▶ Degree를 낮게 가져가는 경우 : 단순한 모델 - 지나치면 과소적합
▶ Degree를 높게 가져가는 경우 : 복잡합 모델 - 지나치면 과대적합
규제 : 모델이 과대적합되지 않게 하는 방법이다.
선형회귀모델에서는 계수를 작게 만들면 과대적합을 피할 수 있다.
∴ 계수(가중치)를 작게 and 비용함수(RSS, Residual Sum of Squares)를 최소화
일반적인 선형 회귀는 RSS를 최소화하도록 회귀계수를 만든다.
여기서 규제를 하면 계수가 작아지는 것이다.
(지난 번에 공부한 내용의 요약이다.)
∴ 규제를 한다는 것 : 계수(가중치)를 조정하겠다는 것!
② L2 규제
가중치를 조정하는 방법 중 하나는 Norm을 이용하는 것이다.
||x||_p = (sum{i=1}^{n} |x_i|^p)^(1/p)
if p=1 : L1 Norm
if p=2 : L2 Norm
이때 L2 Norm을 가지고 가중치를 조정할 수 있다.
ⓐ Cost Functoin을 좀더 유연하게 조정하고
ⓑ 가중치 갱신 식에 적용하여 가중치를 감소시킨다.
일단 선형방정식의 가중치(계수)를 정할 때 가장 큰 목적은 cost를 작게 하는 것이다.
그러나 cost를 최소화하는 것에 너무 집중하면 train_data의 특징에 일반적이게 되어서 과대적합이 일어날 수 있다. 그래서 cost를 '적당히 최소화'해야 한다.
즉, 어느정도의 노이즈(이상치)를 따라가겠다는 것!
그러기 위해 cost를 좀 다른 방식으로 정의해볼 수 있다.
다음과 같다.
new Cost Function = 1/n * sum{i=1}^{n} {now Cost Function + lambda/2 * (||w||_2)^2}
L2 Norm을 now Cost Function에 반영하여 new Cost Function으로 업뎃하고 있다.
(||w||_2)^2 즉 L2 Norm의 제곱을 더했다.
이것의 의미는 즉, 큰 가중치에는 좀 더 크게 반응하고, 작은 가중치에는 덜 반응하겠다는 것이다.
이렇게 이상치에 좀 더 반응하도록 Cost를 조정할 수 있다.
이것이 바로 저번에 배웠던 Ridge다!
Ridge가 바로 이런 L2 Regularization이다.
이렇게 갱신한 new Cost Function을 w로 편미분한 값을 가중치 갱신 식에 사용할 것이다.
가중치를 갱신하는 방법(Optimizer)은 다양한데, 왜인지는 아직 못찾았지만 L2 방법으로 가중치를 조정할 때 SGD(확률적 경사 하강법)을 사용한다.
SGD의 가중치 갱신 식은 w = w - η∇newCost 이다
결과적으로 식을 정리하면
w = (1-ηλ)w - η∇nowCost 이다.
파라미터 η와 λ에 따라 가중치를 적절히 작게 만들 수 있겠다.
간략히 기록하려다보니 살짝 깡총깡총 넘어간 부분이 많다. 잘 이해한지도 모르겠네..
나중에 필요할 때 다시 공부해야겠다.
아무튼 L1규제와 L2규제가 어떤 맥락인지 스캔정도는 해보았다.
▶ 로지스틱 회귀 모델로 다중분류해보자
가장 알쏭달쏭 했던 것을 알게 될 차례!
어떻게 sigmoid가 도출하는 확률값으로 클래스를 다중분류 한다는 것일까?
정말 예상이 하나도 안 갔던 부분이라 궁금했다!!!

회귀모델이 학습한 선형방정식의 형태를 확인해보자.
총 7개의 클래스 Bream, Parkki, Perch, Pike, Roach, Smelt, Whitefish에 대하여 각각의 선형방정식이 만들어진다.
총 7개의 z값이 도출되는 것이다.
그리면 z값을 확률로 변환했을 때 가장 확률이 높은 클래스로 예측하게 된다.

이진분류에서는 sigmoid를 통해 양성클래스에 대한 확률을 반환했지만
다중분류에서는 sigmoid가 아니라 다른 변환식 "softmax"을 사용한다.
softmax
각 클래스의 z값을 0~1 사이 값 s_i로 변환하고,
그것의 전체 합은 1이 되게 한다

softmax를 적용해 확률값을 보자
softmax() 결과 == predict_proba() 결과

오케이.. 여기까지!
로지스틱 회귀모델로 이진/다중 분류를 해냈다!
이전 글: 머신러닝 | 선형회귀모델 규제 - 과대적합 피하기 | 릿지/라쏘 회귀
다음 글: 머신러닝 | 확률적 경사 하강법
관련 글: 로지스틱 회귀 | 선형방정식이 확률p가 되는 과정은?
'데이터분석과 머신러닝' 카테고리의 다른 글
| 혼공단 7기 3주차 미션인증 (0) | 2022.01.30 |
|---|---|
| 로지스틱 회귀 | 선형방정식이 확률p가 되는 과정은? (0) | 2022.01.28 |
| 머신러닝 | 선형회귀모델 규제 - 과대적합 피하기 | 릿지/라쏘 회귀 (0) | 2022.01.24 |
| 머신러닝 | 특성 수를 늘려 과소적합 피하기 - 다중회귀와 특성 공학 (2) | 2022.01.23 |
| 혼공단 7기 2주차 미션인증 (0) | 2022.01.23 |
