
일반적인 선형 상미분방정식은 일반적인 해법이 존재하지 않는다. 풀이가 매번 다르다. 하지만 1차 선형 상미분방정식은 '일반적 해법'이 존재한다.
1차 선형 상미분방정식을 풀어내기 위해 이 '일반적 해법'만 익히면 문제 없을 것이다. 포스팅을 끝까지 읽으면 어느새 1차 선형 미방 풀이의 고수가 되어있을 것..
먼저 1계 선형 미분방정식의 형태에 대한 이야기를 시작하겠다.
1계 선형 미분방정식 "형태"

여기서 알아야 할 것은 표준형이 어떤 형태인가이다.
(1계 선형 미방을 풀기 위해서는 표준형을 잘 알아둬야 한다!)
표준형으로 바꿔주기
보통 알고있는 1차 선형방정식 형태에는 dy/dx의 계수 a1(x)가 붙어있다. 이 선형계수가 1이 아니라면 양변을 선형계수로 나눠서 dy/dx의 계수가 1이 되도록 만들어준다. 그럼 1계 선형 미분방정식에서 y의 계수인 P(x)를 찾을 수 있을 것이고, 이어서 f(x)부분도 찾을 수 있다. (위 이미지 참고)
이때 P(x)와 f(x)를 계수함수라고 부르는데, 이 계수함수 P와 f가 모두 연속이 되는 어떤 구간 I에서 해를 구하게 된다.
자 그럼이제 '해를 구하는 방법'에 대해 이야기할 차례다.
1계 선형 미분방정식 해 구하는 방법 - 두가지
만약에 미분방정식의 형태가 표준형인 dy/dx+P(x)y=f(x)가
ㅇ변수분리형이면 변수분리로 풀면 되고 - 방법 링크
ㅇ변수분리형이 아니라면 '적분 인자'라는 것을 이용한다. - 오늘 포스팅 내용이다.
참고:
선형이고 변수분리형인 미방: dy/dx + 2xy = 0
선형이고 변수분리 불가인 미방: dy/dx + y = x
적분 인자가 뭘까 ─ 적분 인자 이해하기
"> 1계 선형 미분 방정식을 푸는 방법 중에는 '양변에 특수한 함수 μ(x)를 곱해서' 푸는 방법이 있다. 먼저 말하자면 μ(x)가 적분 인자다. 아무튼 이 방법을 통해 식을 전개해나가면 어떻게 되느냐? 적분의 과정을 거쳐서 미분방정식의 해 y(x)를 찾아낼 수 있다. 아직 무슨 얘긴가 싶을 수 있다. 이 얘기를 받아들이려면 다음 과정을 슥 보면 된다.
일단 앞서 배운 미분방정식의 형태인 '표준형 dy/dx+P(x)y=f(x)'을 기억하고 다음 내용을 읽어야 한다.

위 과정을 읽고나서 아하! 했으면 이걸 기억하자!!
ㅡ 1계 선미방 dy/dx+P(x)y=f(x)의 양변에 적분인자를 곱한 방정식의 좌변은 "적분인자 곱하기 y"의 도함수 꼴이다.
이걸 알아야 문제에 적용가능하다. 어떻게 적용가능하느냐? 이따가 예제로 볼 거긴 하지만, 말로 대충 설명해보겠다. step1 ~ step4
step1)
표준형으로 변형한, 또는 이미 표준형으로 주어진 1계 선미방 dy/dx+P(x)y=f(x)에서 P(x)를 파악가능하다.
step2)
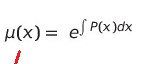
P(x)를 아니까, 적분인자 m(x) = e^integral P(x) dx 를 얻는다.
미분방정식에서 P(x)만 파악하면 바로 적분인자를 얻어낼 수 있는 것이다.
step3)
주어진 미분방정식의 양변에 적분인자를 곱해야 한다. 그러면
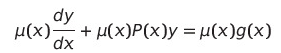
이런 꼴이 나올텐데, 여기서 아까 말한 것을 기억해야 한다!! 좌변이 뭐였는가?
좌변은 d/dx [적분인자 y] 꼴이 자동적으로 된다! 이 말은 즉,
"적분인자를 곱한 방정식의 좌변을
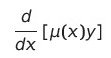
형태로 다시 써줄 수 있다는 것이다!"
이렇게 다시 써줘야 양변을 적분하여 전개가 가능하다.
step4)
이제 양변을 적분하여 y에 관하여 풀면
y(x)를 찾아낼 수 있다!
사실 이렇게 보는 것보다는.. 펜 직접 들고 예제 한두번 풀어보는 게 이해에 훨씬 도움이 된다.
그래서 예제를 하나 안내하겠다.

유의점: x의 범위 설정 : 계수함수 P,f가 모두 연속이 되는 구간 I에서 해를 구하게 되는 거라고 했다.
혹시 읽는 사람 있으면 흔적 하나 남기구 가주세요~~ ㅠㅅㅠ
'수학 > 미분방정식' 카테고리의 다른 글
| 오차함수 (error function) | 여오차함수 (complementary e.f) | 미분방정식(초기값)문제의 해를 오차함수의 항으로 나타내는 방법 (0) | 2021.04.05 |
|---|---|
| 미분방정식 | 특이점에 대하여, 특이점의 위험 | 미분방정식 일반해 구하기 | 구간 (2) | 2021.03.29 |
| 미분방정식 | 간단한 변수 분리 미분방정식 (1계) (0) | 2021.03.29 |
| 1계 변수분리형 미분방정식 | 특이해와 예제 하나 (0) | 2021.03.27 |
| 1계 변수분리형 미분방정식 | 일반해와 예제 하나 (0) | 2021.03.27 |