한빛미디어 도서 <혼자 공부하는 머신러닝+딥러닝>의 전개를 따른 내용이다.
챕터 6, 비지도 학습
* 타깃이 없는 데이터를 사용하는 비지도학습과 대표적인 알고리즘을 소개
* 대표적인 군집 알고리즘인 k-평균과 DBSCAN을 배우자
* 대표적인 차원 축소 알고리즘인 주성분 분석 (PCA)를 배우자
[ 포스팅 목차 ]
1. 주성분 분석 (PCA)
+ 주성분이 가지는 의미 ?
2. PCA로 이미지를 축소하는 과정
3. 축소한 데이터를 복원하기
+ 설명된 분산 (explained variance) ?
4. PCA로 축소한 데이터로 모델 훈련시 이점

# 주성분 분석(Principal Component Analysis, PCA)
: 원본 데이터를 주성분(벡터)로 정사영시켜 차원을 줄이는 방법이다. 원본 데이터를 최대한 보존하며 변환한다.
◎ 이미지 데이터에 PCA를 적용한다면, 이미지 크기를 줄일 수 있다.
이미지의 크기는 픽셀단위로 나타내어진다 (픽셀 = 이미지 데이터의 특성)
참고) 비록 자세한 설명은 하지 않았지만, 아~ 주성분이라는게 수학적으로 이런 의미가 있구나를 상상할 수 있도록 정리해보았다. 선형대수를 배웠거나, 행렬과 고유벡터가 뭔지 알고있다면 주성분이 무엇인지를 개략적으로 이해할 수 있을 것이다.
▶ 주성분의 의미 훑어보기
몇차원이든간에 어떤 원본 데이터가 분포되어 있을 건데, 이 데이터 분포를 행렬로 표현해보자.
예를들면 100x100 픽셀 이미지 데이터를 일렬로 늘어놓은 10000 픽셀짜리 데이터가 N개 있다.
image N개 각각은 10000개의 특성(픽셀, 차원)을 가지고 있다.
(+ 이미지 데이터의 '픽셀'이 데이터의 '특성', '차원'이다.)
| 1 | 2 | 3 | . | . | . | . | . | 10000 | |
| image1 | 0 | 0 | 22 | . | . | . | . | . | 13 |
| image2 | 0 | 19 | 34 | . | . | . | . | . | 15 |
| . | . | . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . | . | . |
| imageN | 0 | 54 | 64 | . | . | . | . | . | 0 |
각 열의 특성값 평균이 0이 되도록 만들어주자. (mean-centered 행렬로 만들자.)
그냥 이 행렬의 요소에다가 각 열의 평균값을 빼주면 된다.
이렇게 센터링한 행렬을 X라고 하자.
[ 공분산행렬 ]
X와 X의 전치행렬을 곱하면 공분산 행렬을 정의할 수 있다.
공분산행렬 = (X^T * X)/n
대각성분은 결국 센터링된 각 특성값 자신끼리 내적한 값이다. 대각성분이 아닌 것들은 서로다른 특성이 내적된 값이다. 즉, 공분산행렬의 각 원소는 두 특성에 대한 분산을 나타내기 때문에 원본데이터의 분포를 잘 설명해준다. 또한 X^T * T이므로 대칭행렬이다.
공분산행렬은 대칭행렬이기 때문에, 직교하는 고유벡터를 갖는다 (정규직교기저를 얻는다).
직교는 일단 차지하고, 원본 데이터를 잘 설명하는 공분산행렬은 고유벡터를 갖고 있다. 이 고유벡터를 주성분(principal component)이라고 한다. 그리고 이 주성분에 데이터를 정사영하면 차원을 낮출 수 있다는 것이 PCA 의미이다.
[ 공분산행렬의 고유벡터 ]
공분산행렬의 고유벡터에 데이터를 정사영했을 때, 분산이 가장 커지게 하는 그러한 고유벡터가 있을 것이다. 그 고유벡터가 '첫 번째 주성분'이다. 그리고 두번째로 분산을 크게 하는 고유벡터가 '두 번째 주성분'이다. 참고로 이 순서는 고유값의 크기와도 연관된다!
만약 어떤 데이터행렬 X에서 만들어낸 공분산행렬에서 고유값이 가장 큰 두 고유벡터를 두 축으로 했다고 하자. 이 평면에 데이터를 사영시켜서 본다면, 두 축에 데이터의 분산이 가장 크도록 사영된다.
[ 대칭행렬의 고유벡터는 직교한다 ]
공분산행렬(대칭행렬)은 직교하는 고유벡터를 갖는다고 한 것을 기억하자. 즉, 두 주성분은 서로 수직이 된다. 데이터를 주성분에 사영해서 만들어진 새로운 데이터는 '새로운 변수(특성)'로 사용될 수 있다. 또한 주성분끼리 수직이 된다는 것은 새로운 변수(특성)간에 관계가 없도록 한다는 것과 의미가 통한다.
주성분은 일반적으로 원본데이터의 특성 개수만큼 찾을 수 있다. 2차원이나 3차원 데이터를 떠올려보면 이해가 갈 것이다. 2차원 데이터에서, 분산을 가장 크게 만드는 주성분 벡터는 2개고 서로 수직이다. 3차원 데이터도 마찬가지로 쉽게 떠올릴 수 있다.
▶ 주성분을 찾은 뒤, 차원 축소는 어떻게 일어날까?
주성분은 원본데이터의 분포를 잘 설명하는 벡터라고 했다.
어떤 10000차원 데이터에서 그러한 주성분을 50개 찾았다고 하자. 각각의 주성분은 10000차원 데이터의 분포를 잘 보여주는 10000차원 벡터이다.
50개의 주성분 각각에다가 데이터를 사영시키자. 그럼 사영시켜 만든 새로운 데이터 50개가 생긴다. 이 말은 즉, 10000차원짜리 원본 데이터 대신에 50차원짜리 새로운 데이터를 이용할 수 있다는 의미다.
다시 말해, 원본 데이터의 분포 특징은 잘 보존한채로 10000차원을 50차원으로 줄일 수 있다!
# PCA로 이미지 축소하기 실습
데이터 불러오기
우리가 사용할 데이터는 10000픽셀(차원, 특성) 이미지 데이터 300개다.
배열(행렬)에는 픽셀값이 들어가있다.
* 일반적으로 이미지 데이터의 픽셀단위가 이해하기 편하겠지만, 차원 또는 특성이라는 용어를 쓰겠다.
ⓐ 찾을 주성분 개수 지정
[ 두 가지 방법 ]
1. n_components 속성에다가 찾을 주성분 개수를 지정하기

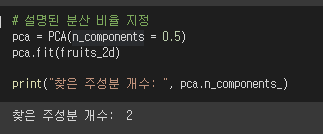
2. n_components 속성에다가 원하는 설명된 분산 비율 지정하기
▶ 이 데이터셋에서 50%의 설명된 분산값을 얻기 위해서는 주성분이 2개만 있으면 된다.
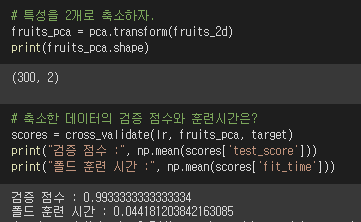
▶ 50%정도의 설명된 분산 값을 가지도록 원본데이터를 축소해보자.
원본데이터는 특성이 10000개였다. 그런데 특성이 2개가 되도록 데이터를 축소시키면 어떨까?
교차검증 점수를 확인해보자.
원본 데이터를 잘 설명하는 단 2개의 특성만 사용해도 99%의 정확도가 나온다! WOW
* 설명된 분산(explained variance): 주성분이 원본 데이터의 분산을 얼마나 잘 나타내는지 기록한 값
puls) 적절한 주성분 개수는? '설명된 분산'개념과 연관된다 (잠시뒤 아래에서 설명)
ⓑ 찾은 주성분 확인해보기
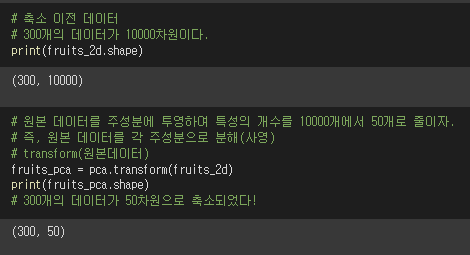
위에서 원본데이터의 분포를 잘 설명하는 50개의 주성분을 찾았고, 이 주성분들은 10000차원이다. 각 주성분의 특징을 확인해볼 수 있도록 100x100 이미지화해보자. (분산이 큰 순서로 50개다.)

ⓒ 원본 데이터를 주성분에 사영시키기
10000차원짜리 원본 데이터를 주성분벡터 50개에 사영시키면 '새로운 특성'이 만들어진다. 이 50개의 새로운 특성(차원)은 원본데이터의 분포 특징을 잘 보존하고 있다.
다시 말해, 이전에는 10000픽셀으로 원본 이미지데이터를 표현했지만, 새로 만들어낸 50개의 차원(픽셀)으로 이미지를 표현할 수 있게 된다.
이것이 이미지 데이터의 축소다!
◆ 50개의 주성분은 얼마나 분산을 잘 유지하고 있을까?

◆ 각 주성분이 갖고있는 설명된 분산 값 확인하기
(차원 축소시 주성분의 개수를 어느정도로 해야하는가?)
분산을 잘 표현한 주성분(앞쪽 주성분)이 대부분의 분산을 표현하고 있다.
참고로, 차원을 얼만큼 감소해야하는지에 대한 이슈는 이 '설명된 분산' 값과 연관된다.
전체 데이터의 분산 중 90% 이상을 표현하는 주성분 개수까지 차원을 감소시켜주는 것이 타당하다고 한다. (출처)
이번 실습에서 50개의 주성분이 표현하는 설명된 분산 비율의 합은 92%이므로 적절한 차원 축소라고 볼 수 있겠다!

# 축소한 데이터를 다시 복원하기
데이터의 특성을 10000개에서 50개로 줄여 표현했기 때문에 데이터의 손실이 존재한다.
헉... 특성을 200배나 줄여서 엄청나게 손실이 되었을 것 같지만, 전혀 아니다!!!!
pca가 새로 만들어 이용한 50개의 특성은 애초에 '원본데이터의 분산을 가장 잘 설명하는 50개의 벡터'다.
∴ 원본데이터 복원력이 우수하다!
▶ 축소한 이미지를 재구성!
PCA 클래스는 inverse_transform이라는 메서드를 갖고 있어서, 축소한 이미지를 다시 복원할 수 있다.
복원 결과, 다시 10000개의 특성을 가지게되었다.
아래의 과일이미지 300개는 10000픽셀로 복원 후 이미지다. 50픽셀짜리를 10000픽셀로 복원했는데 꽤나 잘 복원했다! 만약 주성분을 최대한 많이 사용했더라면 더욱더 원본데이터의 분산을 잘 보존하고 있기 때문에 복원력이 더 좋았을 것이다.




# 축소한 데이터로 머신러닝 모델 훈련시 이점

축소된 데이터의 교차검증 결과를 보자.
검증 점수는 1.0으로 매우 우수하며 폴드 훈련 시간은 매우 짧다!
축소된 데이터의 이점
- 저장공간
- 훈련 속도
이번 내용 정리
- 주성분 분석 (PCA) 소개
- 주성분이 가지는 의미 학습 (공분산행렬의 고유벡터)
- PCA 이미지 축소 실습
- 축소한 이미지를 복원 (+설명된 분산 개념)
- PCA를 통해 축소된 데이터의 이점
◆ 학습에 큰 도움을 받은 글:
https://angeloyeo.github.io/2019/07/27/PCA.html
http://matrix.skku.ac.kr/math4ai-intro/W12/
이전 글:
머신러닝 | k-평균 알고리즘 (KMeans) | 군집 알고리즘
'데이터분석과 머신러닝' 카테고리의 다른 글
| [python] k-means clustering visualization module | how to make scatterplot, gif (0) | 2022.02.17 |
|---|---|
| 혼공단 7기 5주차 미션인증 (0) | 2022.02.17 |
| 머신러닝 | k-평균 알고리즘 (KMeans) | 군집 알고리즘 (0) | 2022.02.14 |
| 머신러닝 | 픽셀 분포의 특징을 뽑아내어 clustering (0) | 2022.02.14 |
| 혼공단 7기 4주차 미션인증 (0) | 2022.02.13 |

