이전 포스팅에서 피보나치 수열 코드를 다음과 같이 설계했었다.
재귀함수 표현으로 작성하면 깔끔할 것 같다고는 생각했지만, 방법을 몰라서 일단 할 수 있는 대로 설계했다.

+재귀함수 표현으로는 어떻게 가능할까?
그래서 공부해봤다!!
재귀함수 표현 공부에 앞서서... 오아..
내가 메서드 활용에 어색한 티가 난다. 메서드를 만들어보자고는 생각을 안했다.
++앞서 내가 프로그래밍한 것처럼, 이전에 계산했던 값을 저장해두었다가 나중에 재사용하는 방법이 동적 프로그래밍의 방법중 하나라고 한다. (Dynamic programming)
++또한 피보나치 수열이 재귀함수의 활용이나 동적 계획법을 연습하는데 흔히 쓰인다고 한다. 오~!! 그런데 내가 이걸 스스로 연습해볼 생각을 하다니 내가 너무 기특하다. 앞으로도 이런 태도를 가지자 후훗
먼저, n번째 피보나치 수를 구하는 fibo함수를 다음처럼 정의하자.

기본 재귀적 풀이
>> 수열의 정의에 충실하여 가장 구현하기 쉬운 재귀적 풀이이다.
위에서 만든 fibo함수를 그대로 구현하기!
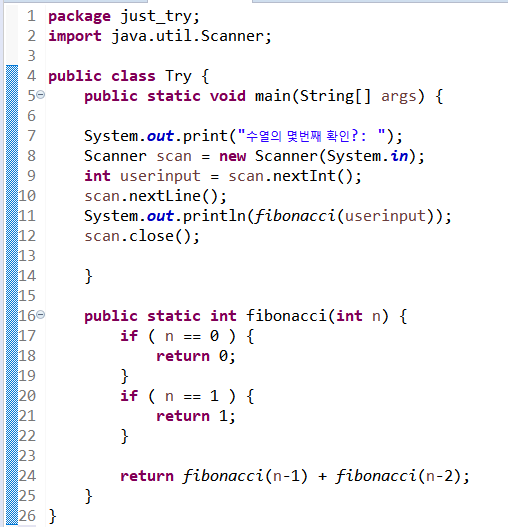
재귀함수를 그대로 구현했다.
+아이고 왕초보얏 메서드 만드는 거에 익숙해지자^o^;;!!!
생각을 할 줄 알아야 할 거 아냐!!!!!
!!단점!!
위의 메서드는 성능면에서 매우 좋지 않다. 리턴을 연쇄적으로 하기 때문이다... 너어무나 비효율적이다.
만약 n이 4일때를 보면
fibonacci(4)는 fibonacci(3)+fibonacci(2)를 리턴하고 이 각각의 fibonacci(3), 그리고 fibonacci(2)는 또..또..
각각 fibonacci(2)+fibonacci(1) 그리고 fibonacci(1)+fibonacci(0)을 리턴하고 .. 또 또 저 fibonacci(2)는 또...
fibonacci(1)+fibonacci(0)을 리턴한다....
휴 이렇게 연쇄적으로 리턴리턴을 하니 성능이 좋겠는가!!!!!
즉 위의 피보나치 메소드의 시간복잡도는 n이 1씩 증가할 때마다 2배씩 늘게 되어서, O(2^n)이 된다.
함수가 한 번 호출되면 다시 두 번 호출되기 때문에 지수적으로 증가해 O(2^n)이 된다.
와우!! 너무 심각하게 비효율적.
(2배라는 대략적인 느낌은 오는데 엄밀한 증명이 궁금하긴 하다.)
그래서 무난하고 성능이 좋은 동적 프로그래밍을 사용하는게 효율적이라고 한다.
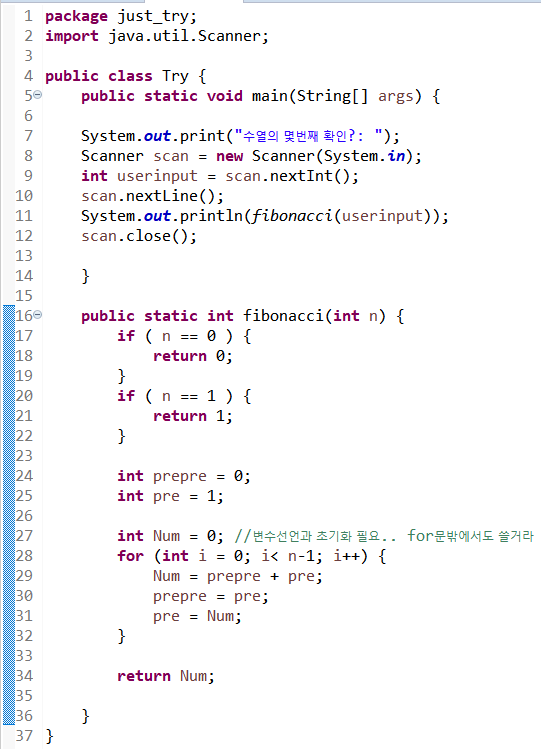
이정도가 깔끔한 듯하다.
'기타' 카테고리의 다른 글
| 네이버 이미지 크롤링 [Python] (0) | 2020.08.29 |
|---|---|
| 히 책왔다 (0) | 2020.08.28 |
| 피보나치 수열 프로그램 만들어보기 | 재귀X (0) | 2020.04.19 |
| [비주얼 스튜디오] 콘솔 실행파일(exe)만들기 / "빌드를 통해서" | 2017, 2019 (5) | 2020.03.02 |
| Hello Coding 헬로코딩 프로그래밍 챕터10; 기초문제 (0) | 2020.03.01 |