[ 관련 글 ]
■ 전송 마이크로연산
[컴퓨터구조] Register Transfer 연산 의미, 그리고 BUS설계가 중요한 이유와 설계방법 | 하드웨어
■ 산술 마이크로연산
[컴퓨터구조] Binary Adder, 그리고 Binary Adder-Subtractor | 컴퓨터의 산술 연산 구조 | 하드웨어
[컴퓨터구조] Binary Incrementer | 컴퓨터의 산술 연산 구조 | 하드웨어
[컴퓨터구조] Arithmetic Circuits | 컴퓨터의 산술 연산 구조 | 하드웨어
■ 논리 마이크로연산
[컴퓨터구조] Logic Micro-operations | 컴퓨터의 논리 연산 구조 | 하드웨어
■ 이동 마이크로연산
[컴퓨터구조] Shift Micro-operations | 컴퓨터의 shift 연산 구조 | 하드웨어
이번 포스팅에서는 이동 마이크로연산 (Shift micro-operation)과,
그러한 shift연산을 하드웨어적으로 어떻게 구현하는지 그 회로를 확인해보자.
[목차]
▶ Shift micro-operation
▶ Shift micro-operation 종류
- 그 중 Artimetic shift left를 유의깊게 봐야 할 이유
▶ Shift연산 회로의 구조 확인해보기
Shift Micro-operations란?
레지스터의 비트 간 행해지는 연산을 micro-operation이라고 한다.
(micro-operation에 대해 더 자세히 보기: 이 링크 윗부분을 읽으세요!)
그중에서 오늘은 Shift(이동) 마이크로연산에 대한 것을 공부해보자.
비트연산 shift는 다들 알고 있을 거라고 생각한다.
Shift Micro-operations 종류
shift micro연산은 크게 세 가지 류가 있다.
- Logical shift : shift 후에 비어있게 되는 비트 부분이 0으로 채워진다.
- Circular shift : shift 후에 밀려나는 비트 부분이 다시 순환(rotate)된다.
- Arithmetic shift : 부호 비트는 shift되지 않는 방법이다.
이러한 shift 연산의 종류와 그 기호를 나타내면 이렇다.
| 기호 | 설명 |
| R <- shl R | Shift-left |
| R <- shr R | Shift-right |
| R <- cil R | Circular Shift-left |
| R <- cir R | Circular Shift-right |
| R <- ashl R | Arithmetic Shift-left |
| R <- ashr R | Arithmetic Shift-right |
*화살표 연산자 <-는 transfer-register micro연산의 연산자이다. 잘 모르겠다면 여기로
▷ Logical shift는 딱히 설명할 것은 없다.
▷ Circular shift도 딱히 설명하고싶은 건 없다.
▷ Arithmetic shift 얘는 좀 이야기하고 싶다. 주의사항이 있어서다.
Arithmetic shift left
right shift와 left shift의 결이 좀 다르다.
컴퓨터의 아주아주 최악으로 가장가장 심각한 문제가 overflow 문제인데 left shift의 경우 overflow가 나타날 수 있다. 반드시 그러한 치명적인 조건을 파악하고 방지해야만 한다. 바로 알아보자.
일단, right shift는 부호비트를 유지하지만 left shift는 부호비트를 유지하지 않는다.
아래 링크(위키) 들어가면 사진 있는데, 참고!
https://ko.m.wikipedia.org/wiki/%EC%82%B0%EC%88%A0_%EC%8B%9C%ED%94%84%ED%8A%B8
산술 시프트 - 위키백과, 우리 모두의 백과사전
기호로는 보통 ≪ , ≫ {\displaystyle \ll ,\gg } 가 사용되며 a ≪ n {\displaystyle a\ll n} 의 형태로 표시된다. 이 연산의 의미는 컴퓨터의 메모리에 저장된 2진법 숫자를 n비트만큼 좌 또는 우로 이동하
ko.m.wikipedia.org
- right shift할 경우: 오른쪽으로 shift되면서 비게 되는 비트자리는 부호비트와 동일한 비트로 채워진다. 부호비트가 0이면 0으로 채워지고, 부호비트가 1이면 1로 채워진다. right shift는 두배 나누기하는 연산으로도 볼 수 있다. 이 경우에는 아무 문제 없다.
- left shift할 경우: overflow가 발생할 수 있다.
이건 예를 들어 설명하겠다.
8비트 레지스터에 이런 값이 저장되어 있다고 하자.
[ 1001 1100 ]
이 값은 10진수로 -100이다.
----------접은글 시작
이 접은글은 안 봐도 되는데, 혹시 1001 1100이 왜 -100인지 궁금한 분들을 위해서..
[ 1001 1100이라는 음의 이진수를 10진수로 변환하는 방법 ]
1단계: 2의 보수 처리를 한다.
0110 0011 + 1
0110 0100
2단계: 이제 10진수로 변환해보면 된다.
4+32+64 = 100
3단계: 마지막으로 -부호를 붙여주면 끝
-100
설명은 했지만, 아주 기본적인 내용이니 반드시 알아야 한다.
----------접은글 끝
이것을 left shift하면
[ 0011 1001 ]이 된다.
이 값은 10진수로 +56이다.
- 원래 맨 처음에 주어진 값인 -100이라는 값을 left shift하면 x2배가 되어서 -200이어야 한다.
하지만 8진수 sign값의 범위는 -128~127이다. 그래서 우리가 의도했던 값인 -200은, 사실 8진수 sign 비트가 표현불가능한 값이었다. 즉 overflow가 일어날 수밖에 없었다.
-100을 left shift하여 56이 나왔는데, 참고로 -128x2=-256에 +56을 더하면 -200이 나온다.
- 우리가 의도했던 연산결과인 -200을 표현하려면 8개의 비트로는 부족하다. 이렇게, 값을 표현하기 위해 추가적인 비트가 필요하다면 overflow다.
만약 8비트가 아닌 16비트 레지스터였다면 overflow 없이 정상적으로 이루어진다.
혹시 그 과정을 보려면 더보기 클릭.
----------접은글 시작
100의 보수 -100을 만들어보자.
0000 0000 0110 0100 [100]
1111 1111 1001 1011 [100의보수 +1]
1111 1111 1001 1100 [100의 2의보수]
이 값이 100의 보수인 -100이다.
x2를 하기 위해 left shift하면
1111 1111 0011 1000이다. 이 값은,
0000 0000 1100 0111 +1 [보수처리 +1]
0000 0000 1100 1000 [2의 보수]
이 값은 10진수로 200이다.
결과적으로 -부호를 붙이면 -200이다.
16비트 레지스터였다면 overflow가 발생하지 않고 -100의 left shift 결과 -200이 된다.
16비트로 표현할 수 있는 값의 범위에 들어가기 때문이다.
----------접은글 끝
결과적으로, 최상위 비트 2개가 서로 다르면 left shift했을 때 overflow가 발생한다. (필요충분조건임)
이렇게 생각하면 쉽다.
01XX XXXX라는 값은 가장 큰 양수에 가까우므로, 이걸 x2하면 overflow다.
10XX XXXX라는 값은 가장 작은 음수에 가까우므로, 이걸 x2하면 overflow다.
정리: Arithmetic shift 연산에서 left shift를 할 경우 overflow가 발생할 수 있다. overflow의 필요충분조건은 최상위 비트 2개가 서로 다른 상황일 때다. 그래서 left shift 연산을 하기 전에 최상위의 두 비트를 체크해보면 된다.
combinational circuit shifter
이동 연산을 수행하는 회로를 확인해보자.
shift 회로는 간단하다.
Select가 0이면 shift right, 1이면 shift left를 한다.
그 Select넘버가 x1사이즈의 MUX에 들어간다.
레지스터 A에 있던 비트의 나열이 A0 A1 A2 A3라고 해보자.
0이면 shift right이므로 총 4개의 MUX에서 각각 I_R, A_0, A_1, A_2가 출력된다.
1이면 shift left이므로 총 4개의 MUX에서 각각 A_1, A_2, A_3, I_L가 출력된다.
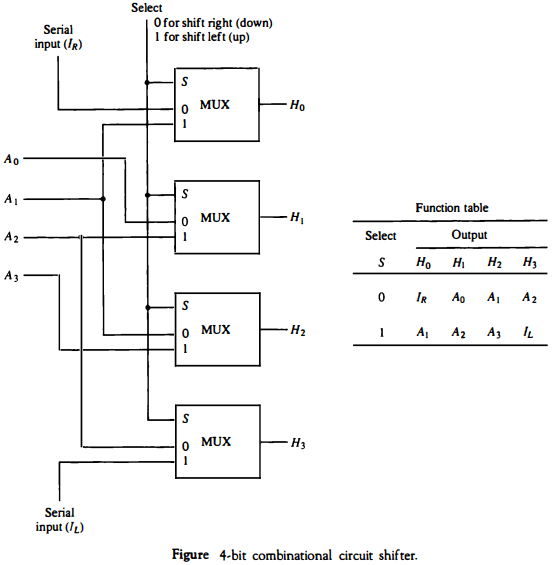
그냥 이게 전부인 간단한 회로다!
'컴퓨터구조 & OS' 카테고리의 다른 글
| [컴퓨터구조] 16비트 컴퓨터 설계하기 - 레지스터를 정의하자 (0) | 2021.10.13 |
|---|---|
| [컴퓨터구조] 16비트 컴퓨터 설계하기 - 명령어 코드의 구조 | Instruction Codes (0) | 2021.10.12 |
| [컴퓨터구조] Logic Micro-operations | 컴퓨터의 논리 연산 구조 | 하드웨어 (1) | 2021.10.11 |
| [컴퓨터구조] Arithmetic Circuits | 컴퓨터의 산술 연산 구조 | 하드웨어 (0) | 2021.10.11 |
| [컴퓨터구조] Binary Incrementer | 컴퓨터의 산술 연산 구조 | 하드웨어 (0) | 2021.10.11 |