드디어 교육관련측도와 정보격차측도의 상관관계를 하나 찾았다.
거의 맨땅에 헤딩하려니까 힘들다.. 앞으로 언제 어떻게 의미있는 분석결과를 보게될지 막막하기도 하다.
발표까지 8일 남았다.
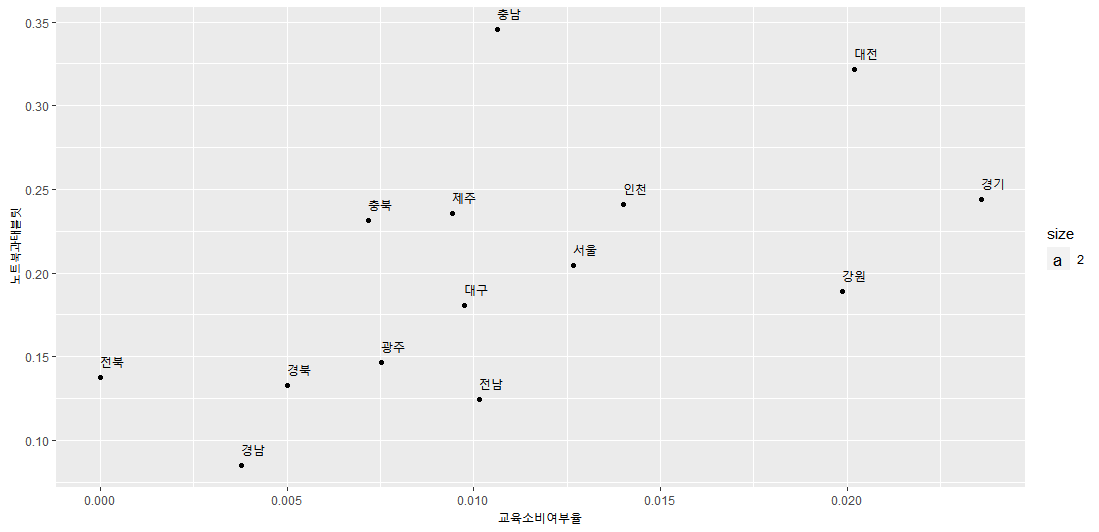
일단 모든 지역에 대한 산점도는 아래와 같다.
일단 이 상관분석 결과는 의미가 없었다. 하지만 나는 의미있는 결과를 봐야 했다.
세종, 부산과 같은 결과를 제외하면 어느 정도 양의 상관관계처럼 보이는데, 실제로 제외하면 어떨지 궁금했다.

일단 지난 시간에 나는
사교육비 지출이 많은 상위지역과 하위지역을 선정한 바 있다.
사교육비상위지역: 서울, 경기 | 세종, 인천, 대전, 대구
사교육비하위지역: 경북 | 강원, 경남, 충북
그렇다면 이 상위지역과 하위지역에 포함시키지 않은 나머지는 일단 위 산점도 결과에서 제외시키고 보아도 의미있는 산점도이지 않을까 생각했다. 일단 사교육비 지출이라는 측도로 지역을 나누기로 앞서 결정했기 때문이다.
그런 교육 측도로 미리 선정한 지역을 대상으로 또다른 교육측도와 정보격차측도의 상관관계를 바라봐도 아무 문제 없지 않을까 하는 생각을 하며.. 위 지역들만 포함해보기로 했다.
다소 극단에 있어보이는 세종과 부산을 제외했더니 p-value가 0.05를 살짝 넘는다.
그래서 지역 하나를 더 제외하고 바라보았다. 울산.

p-value가 0.03395가 나온다.
작은 p-value를 왜이렇게 보기 힘든지..
주제 방향을 잘못 골랐나 데이터를 잘못 선정했나 약간 지친다 ㅜㅜ
아무튼
그리고 대상지역만을 대상으로해서도 산점도를 그려봤다.
단, 극단에 있는 것 같은 세종은 제외했다.
(세종을 포함하더라도 p-value가 0.5를 사알짝 넘는 정도다.)


p-value가 0.03정도 된다.
드으으디어 이 교육소비비율과 기기(노트북,태블릿)보유율이 보이는 양의상관계수가 유의하다고 말할 수 있다.
기기를 태블릿+노트북으로 보지 않고, 태블릿 기기보유율만 따져보자.
그리고 교육측도로는 교육이용비율을 넣어보자.


이 경우는 의미 없다.
그런데 나는 의미 있는 결과를 봐야 해서.. 저 극단에 있는 경남과 광주를 제외하고 다시 따져봤다.
사실 이렇게 해도 되는지는 잘 모르겠다. 그런데 시간이 얼마 안남아서 제외하겠다.
제외하는 나름의 이유는.. 일단 경남과 광주는 이전에 교육측도(사교육비)로 상위/하위로 선정한 핵심 대상 지역이 아니라서이다.
극단의 두 지역을 제외하고 다시 따져본 결과


ㅠㅠ p-value가 0.02705로 나왔다!!
아 배고프다.. 내일은 추석이니 잘 먹어야지 ㅜ,ㅜ
아무튼 그게 아니라.. 기쁘다.
사실 노트북이나 스마트폰같은 기기는 보급률이 지역과 상관없이 전체적으로 높아서 측도로 사용하기에는 살짝 아리송한 느낌이 있었는데, 태블릿이라는 기기는 구매목적이 뚜렷한 기기라고 생각한다. 구매하는 사람이 모두 교육목적인 것은 아니지만, 학생이 태블릿을 구매하는 이유 중 큰 비중을 차지하는 것이 학습이 아니겠나?!
다행히 지역별 태블릿보유율과, 온라인교육을 이용하는 비율이 의미있는 양의 상관관계를 보였다.
적당한 기기보급이 필요한 이유를 설명가능할 것 같기도 하다.
또한, 저번에 사교육측도로 선정한 지역 극상위인 서울,경기/ 그리고 극하위인 경북을 위주로 보면,
서울, 경기는 다소 교육이용비율과 태블릿보급률이 모두 상위권이고, 경북은 모두 하위권이다.
사실 지난 측도로 선정한 극상위, 극하위가 아닌 나머지 지역들은 애매하지만,
극상위, 극하위인 서울경기와 경북은 이렇단말이다.
'데이터분석과 머신러닝' 카테고리의 다른 글
| 혼자 공부하는 머신러닝+딥러닝 | 도서 추천도 하고 내 얘기도 겸사겸사.. (0) | 2022.01.10 |
|---|---|
| 오예~! (0) | 2021.11.15 |
| R데이터분석 | 사교육측도 둘 사이의 상관관계 - 결론: 상관관계 없다. (0) | 2021.09.15 |
| R데이터분석 | 박스플롯에서 이상치 확인 (0) | 2021.09.15 |
| R데이터분석 | 분산분석, 사후분석으로 지역별통계량 분석 (0) | 2021.09.15 |