합병정렬의 시간복잡도는 O(NlogN)
(또는 세타(NlogN)) 이 사실은 다들 알고 있을 겁니다.
그리고 이 O(NlogN)이라는 복잡도를 어떻게 따지느냐? 다들 한번쯤 해봤을 것입니다.
혹시 깔끔한 이해 없이 지나갔다면 다시 한번 천천히 해봅시다
그 전에! 분할정렬 자체에 대한 개념이 모호하신 분은 이 포스팅을 읽고 다시 돌아오는 것을 추천합니다.
시작!!
아래 그림 많이 보셨을 겁니다. 합병정렬!!

이 합병정렬의 복잡도가 왜 NlogN인지 차근차근 설명할텐데요,
순서대로 사고하면서 천천히 해봅시다
먼저, 절반으로 분할해가는 과정을 봅시다.

- 초기 배열의 요소수는 N개입니다.
- 분할정렬 함수의 인자로는 "배열", "p", "r"이 들어옵니다.
p는 분할대상인 요소가 시작하는 인덱스였죠. 초기 함수의 인자로 0이 들어갑니다.
r은 분할대상인 요소가 끝나는 인덱스였죠. 초기 함수의 인자로 N-1이 들어갑니다.
- 총 N개요소가 있는 배열을 반(1/2)으로 쪼개고, 쪼개고, 쪼개며 결국 요소 한개단위로 따지게 됩니다.
그런데 이렇게 반으로 쪼개고 쪼개고.. 하는 과정은
q = floor((p+r)/2)에의해서 이루어집니다.
단순한 대입연산이죠.
인자로 들어가는 p, r에 의해 q를 단순히 연산해주고
q를 기점으로 반으로 뚝 자른 배열들을 대상으로 다시 재귀호출을 하는 것의 연속입니다.
즉, 걸리는 시간은 그냥 상수시간이죠!
일단 분할정렬 함수 MergeSort가 몇번 재귀호출 되느냐는 차치하고, 배열을 Divide하는 시간이요. 상수시간이죠.
그럼 여기는 그냥 상수시간이니 넘어가고,
하나하나 쪼개진 상태에서부터 Merge해가는 과정을 집중해서 봅시다.
Merge 과정
첫번째,
NlogN에서 logN의 이해

- 하나하나의 조각들을 다시 합치고 정렬해서, 다시 N개의 요소를 가진 배열로 만들어야 합니다.
- 하나하나의 조각들은 어떻게 조각난 거였나요? 처음 요소수 N을 절반으로 뚝뚝 잘라 만든 거였죠. "절반, 즉 1/2을 해온 결과입니다."
- 그럼, 하나하나의 요소를 다시 N개의 요소로 합치려면 다시 2배.. 2배... 해가야겠죠!
- 하나로 쪼개진 요소가 N개의 요소가 되는 이 과정은 "몇 회"인가요?
- 즉, 두배 곱하는 것을 몇번이나 해야 하나요?
하나의 원소를 몇번 2배해야 전체요소수 N을 되찾을 수 있겠느냐를 따져보아야겠습니다.
2^x = N에서 x를 구하면 되겠죠.


요소 '한개'에서 x번 두배 곱해나가야 원래요소 N개를 되찾을 수 있구나!!
여기서 아하~ 하실 수도 있지만, 아직도 의아할 수도 있죠.
복잡도 N*logN에서 N에다가 이 logN을 곱했는데, 왜 실제 재귀호출 횟수를 곱하는 게 아니라, 하필 2배하는 횟수인 logN을 곱하는 거야? 라고요! 아무리 x=logN을 '층 수'로 본다고 쳐도, 이 층 수가 재귀호출에 의미가 있는지 의아하게 생각할 수도 있죠. (사실 제가 그랬어요..!)
지금부터 설명할게요. 이건 분명히 재귀호출하는 정도로 따질 수 있는 부분이에요. 왜냐구요?
원래 배열의 길이를 1/2하면서 재귀호출이 이루어졌기 때문이죠. 좀 더 자세히 설명해볼까요?
원래 요소수가 N인 배열 하나가 통채로 들어오면, 그것을 반으로 쪼개고 쪼개며 재귀호출을 했었죠. 그럼 맨 처음에 퉁으로 N개 묶음으로 생각하던 배열을 점점, N/2개단위, N/4단위, N/8개단위... N/2^x개단위로 다루게 되죠. 우리가 다뤄야 하는 요소수를 점점 반으로 쪼개가는 거예요. 그래서 결국 하나 단위로 보게 되죠(base-case). 그럼 결국 N/2^x=1을 풀면 x=logN임을 알 수 있습니다.
그래서 logN이라는 것을 재귀 레벨로 따져볼 수 있는 것입니다. recurrence equation인 T(n)을 따져보면 T(n)=Θ(NlogN)인데요, Merge sort에서 Combine이나 Divide하는 복잡도를 차치하고, 재귀호출해가는 것에 집중해서 봅시다. 일단 Merge Sort 특성상 '두개로 쪼개요'. 두개로 쪼개는데 개수도 절반으로 쪼개죠. 그래서 T(n)은 2*T(n/2)으로 나누어 풀고, T(n/2)는 2*T(n/4)로 나누어 풀고, T(n/4)는 2*T(n/8)로 나누어 풀고.. 그러거든요? 언제까지 이러냐구요? T(1)에 다다를 때까지요. 그럼 아까 설명했듯이 n/2^x=1에서 x=log(n)입니다. 사실 위 문단에서 다 한 얘기죠~!
이렇게 recurrence equation 측면에서 보면 log(n)이 재귀의 복잡도를 설명할 수 있음이 확실히 보이죠? 그래서 다른 재귀함수의 복잡도와 비교가능하기도 하고요.
아무튼! 두배하는 과정을 총 x번 해야한다는 것을 알았습니다.
x = logN인 것도 알겠고요. 그게 재귀호출의 레벨을 나타낸다는 것도 알겠어요.
그런데 NlogN의 N은 어떻게 나온 걸까요?
이건 더 쉬워요.
두번째,
NlogN에서 N의 이해
합병된 각 층에서 재정렬(Merge)을 하잖아요?
여기서 재정렬하려면 결국 각 level에서는 모든 데이터를 비교연산합니다. 즉 N회요!
N은 바로 이 N을 이야기하는 겁니다.
여기서 바로 이해가 갈 수도 있지만, 좀 더 설명해볼게요!
일단 간단히 Merge함수의 과정을 의사코드로 살펴봅시다.

첫 번째 for문을 봅시다.
for i <- 1 to n1
do L[i] <- A[p+i-1]
for j <- 1 to n2
do R[j] <- A[q+j]첫 번째 for문의 실행횟수는 어떻게 될까요? 다음과 같습니다.
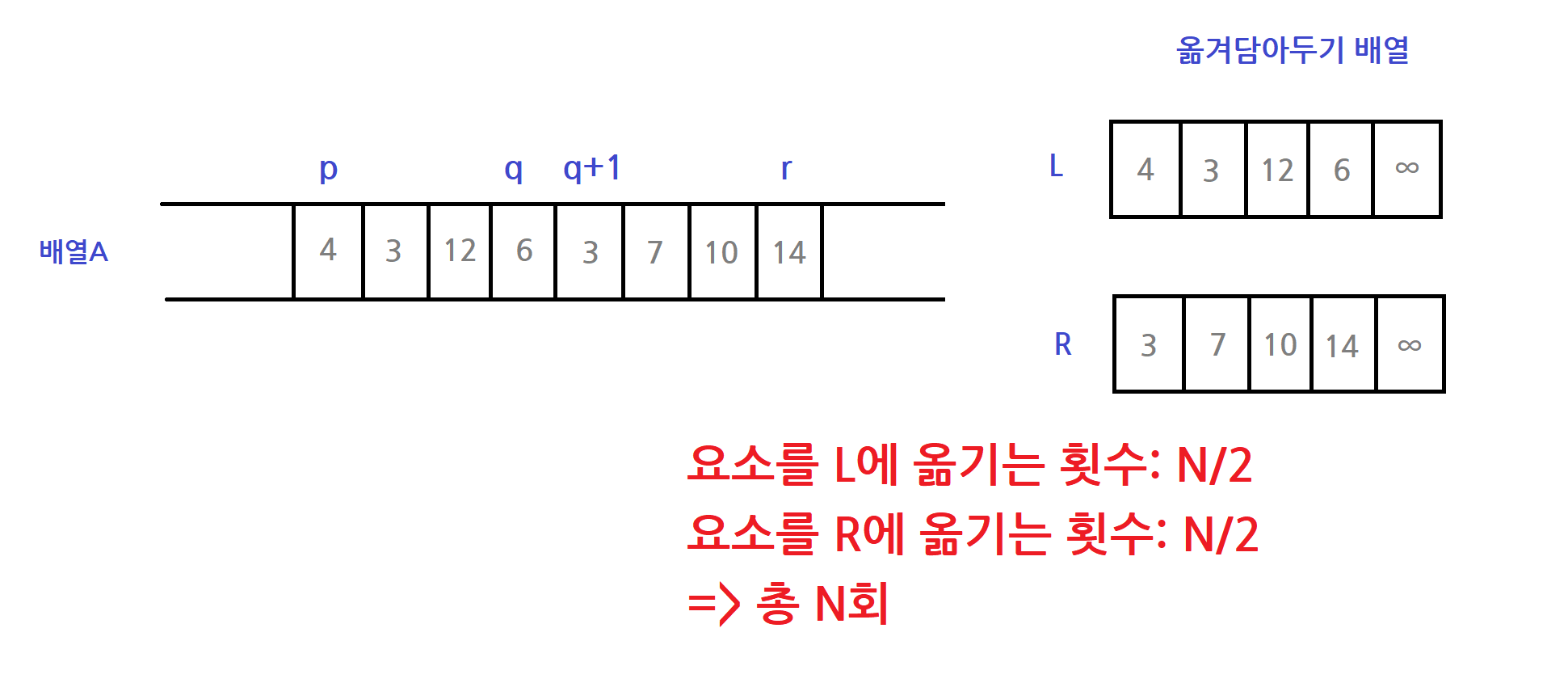
이제 두 번째 for문을 봅시다.
for k <- p to r
do if L[i] ≤ R[j]
then A[k] <- L[i]
i <- i+1
else A[k] <- R[j]
j <- j+1
실행횟수는 어떻게 될까요?
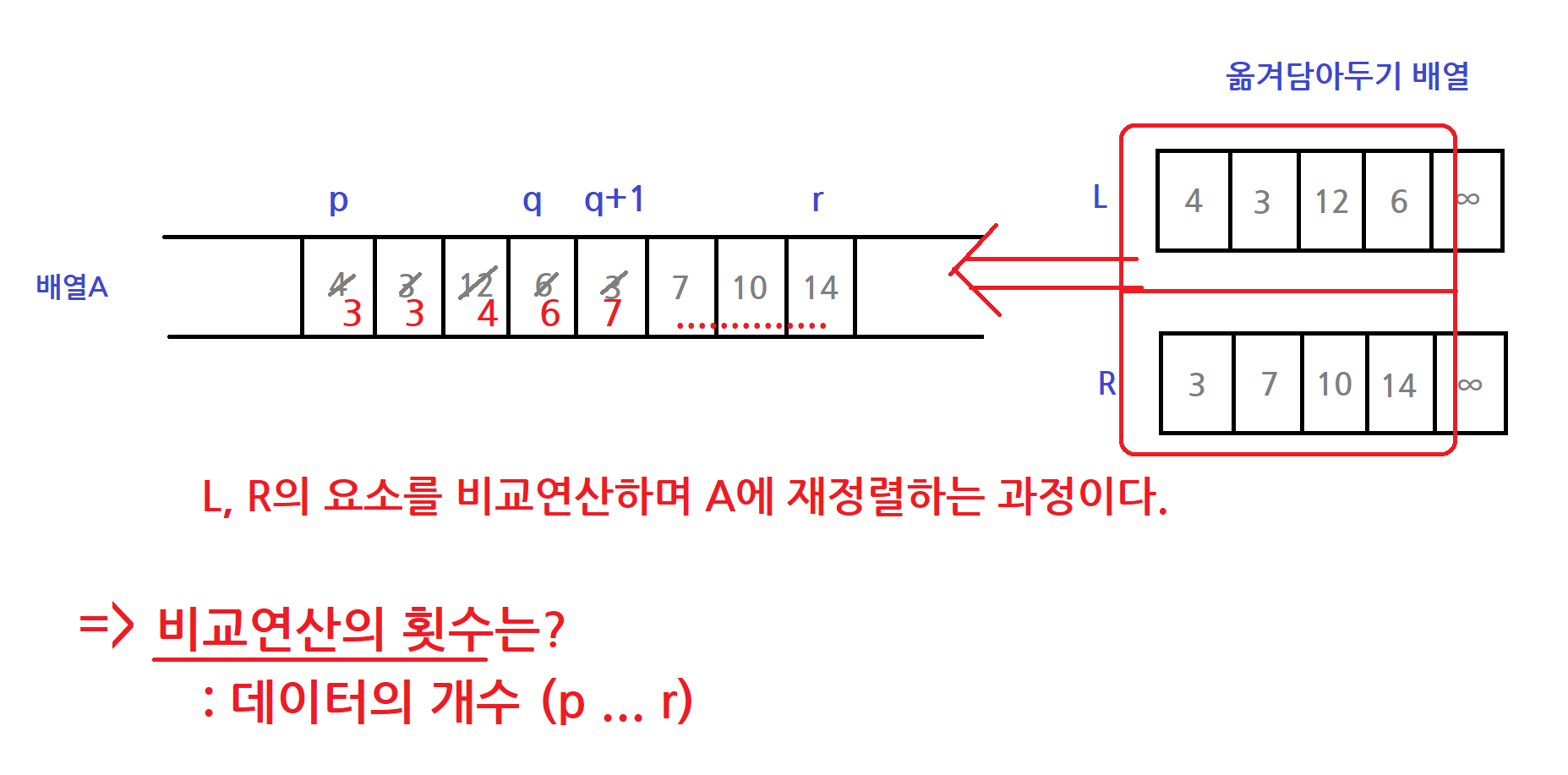
잠깐..
Merge의 input으로 들어오는 부분들은 모두
N에서부터 반(1/2)으로 몇번 쪼개온 부분들이라는 걸 기억해보세요.
그러면 아래와 같은 이유로, 각 층에서 비교연산하는 횟수는 N으로 동일하다는 것이 보입니다.
이렇게 우리는 각 층마다 모든 데이터를 비교연산하게 됩니다. 모든 데이터를 합병정렬해야하기 때문이죠.
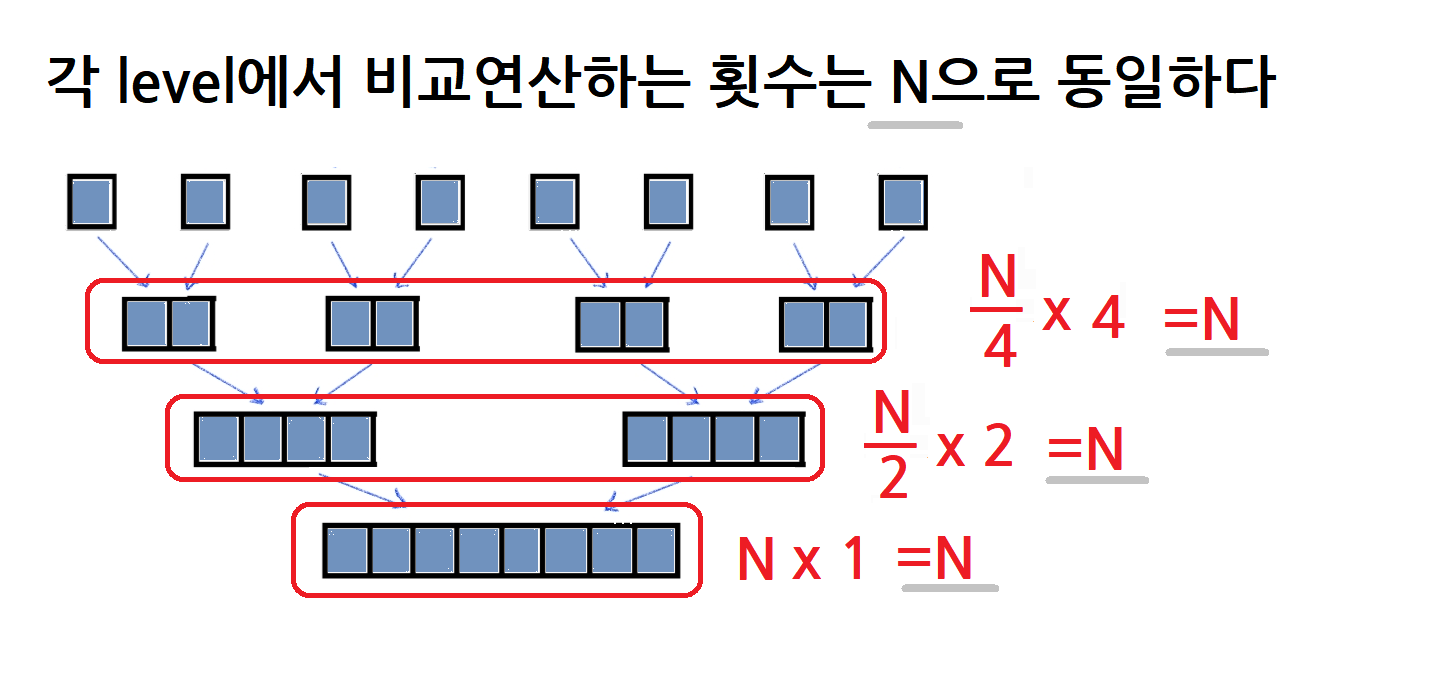
총 2개의 for문 모두에서 복잡도가 N을 넘어서지 않네요.
그럼 일단 하나의 층에서 Merge과정에 대한 복잡도는 O(N)입니다.
이제 다 됐습니다.
그럼 합병정렬 전체의 복잡도는 어떻게 될까요?
전체적으로 이루어지는 재귀의 정도는 뭐였죠? 즉, 쪼개가는 과정이 어느정도로 있었죠? logN번입니다.
각 층마다 비교연산(정렬)은 몇번 이루어지죠? N번입니다.
둘이 곱하면 복잡도가 NlogN으로 설명되는 거죠!
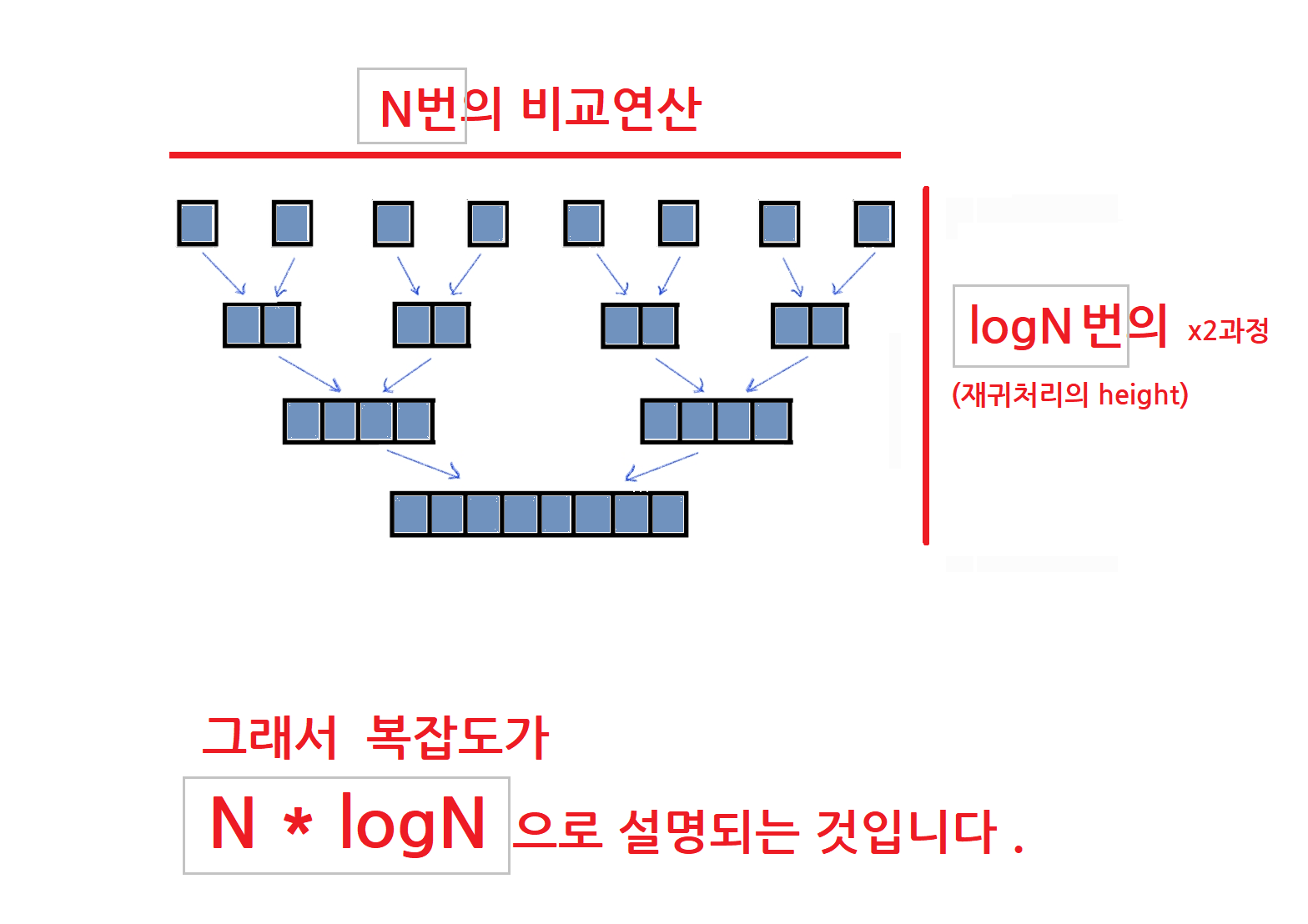
이상 마칩니다.
참고: recurrence equation 측면의 부가설명:
recurrence equation은 다음과 같습니다.
T(n) = 2*T(n/2) + Θ(n)
여기서 Θ(n)이 바로 Combine(합병)하는데 걸리는 시간이죠.
2*T(n/2)는 재귀호출되는 부분인데, T(n/2)는 결국 2회 있게 되므로 2를 곱해주는 형태입니다.
n/2일 경우에도 마찬가지입니다.
T(n/2)=4*T(n/4) + Θ(n/2)
참고로, Divide할 때 걸리는 시간은 Θ(1)인데요, 상수이므로 덧셈하지 않고 생략합니다.
왜 Divide에서 상수시간 걸린다고 했었죠? q만 단순연산하면 되기 때문이었죠!
이렇게도 한번 봅시다.
T(N)에서
- Combine하는 횟수는 x=logN이고,
각 level은 x+1=logN+1입니다.
- 정렬하는 횟수는 N입니다. 아까 봤죠!
그래서 총 실행횟수는 N(logN+1)=NlogN+N
그래서 recurrence equation은 T(N)=Θ(NlogN+N)=Θ(NlogN)입니다.
도움이 되셨으면.. 공감버튼을 눌러주세요!
'자료구조 + 알고리즘' 카테고리의 다른 글
| [자료구조] Binary Tree (1) | 2022.11.29 |
|---|---|
| Queue 구조 실습 | client and server Simulation (0) | 2022.05.20 |
| 알고리즘 | 합병 정렬 (Merge sort)과 분할정복알고리즘 | 코드 설명 (0) | 2021.09.08 |
| 알고리즘 | 삽입정렬(Insertion Sort) | 코드 설명 (3) | 2021.09.08 |
| 재귀함수를 비재귀적으로 구현하기 예시 - 재귀함수 동작의 이해를 높이자 (4) | 2021.07.14 |
